
In his latest column, PDC Stats Analyst Christopher Kempf evaluates the concept of 'REAL averages' and how they compare to actual match averages...
In April, Pascal Rupprecht won a first-round Players Championship match with an 81.89 average, defeating Martijn Dragt 6-5 even though the latter averaged 94.64, making it the largest averages deficit for a winner of a Players Championship match seen thus far in 2024.
There have been 505 such matches this year in which the leader in points scored per dart thrown was not the winner of the match - nearly 25% of the total.
Losing a leg is often advantageous to one's averages, especially in the highest levels of darts. Not attempting finishing doubles means that treble 19s and 20s make up a larger percentage of the total points represented in the three-dart average.
At the greatest theoretical extreme, a player averaging 158.63 could lose a best-of-11 match to a player averaging 77.08, and a player could be whitewashed 6-0 despite having an average 17 points higher than that of his opponent.
Alternative statistics in darts try to use other aspects of a player's game, like checkout percentage or last-dart-at-double accuracy, to compensate for the fact that the topline statistic in darts is so heavily biased in favour of one aspect of the game.
But it's also to extrapolate from the three-dart average to estimate what a player would have averaged in a leg that they lost, were they forced to play that leg until the point of checkout, no matter how long it took.
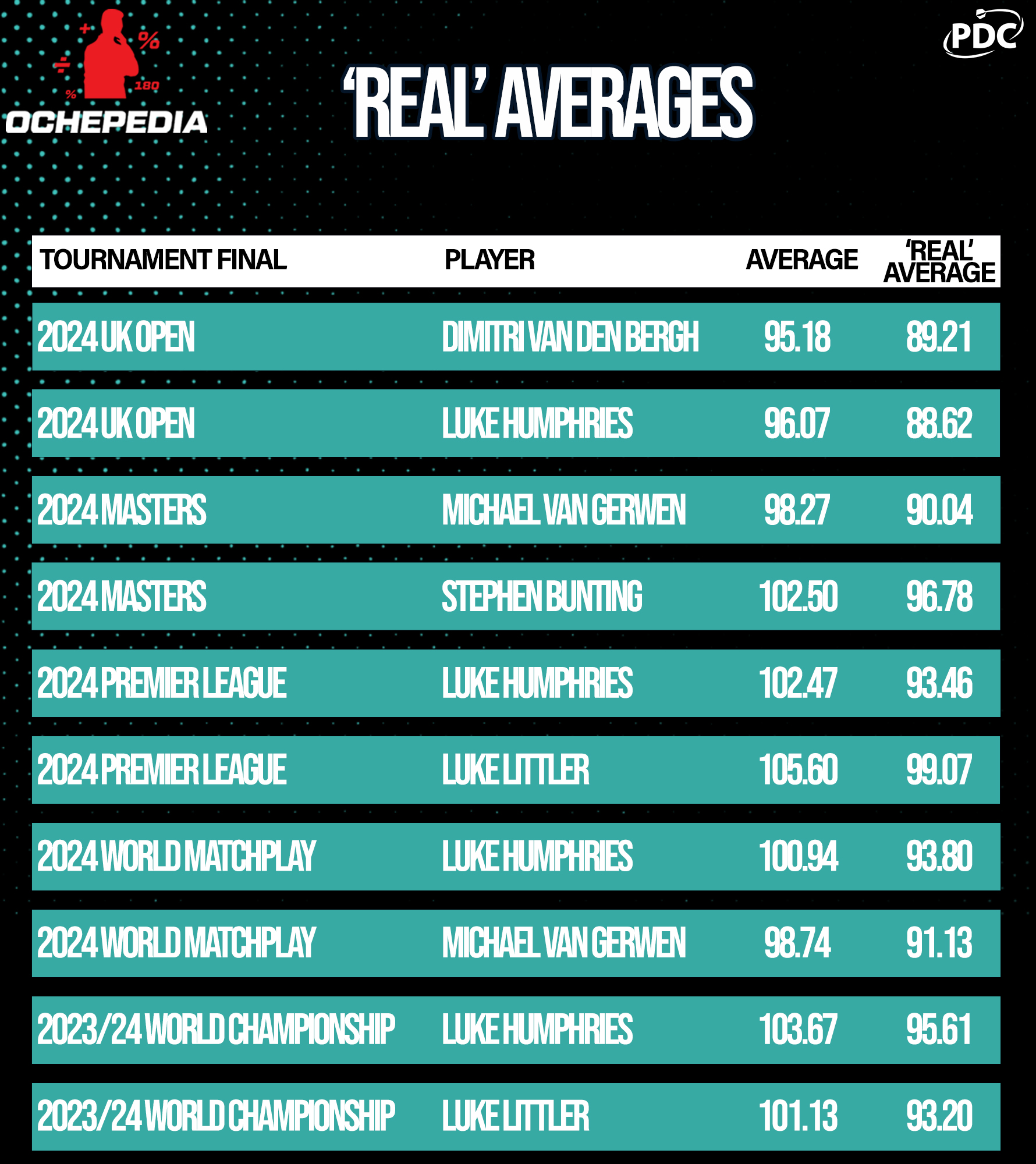
The concept of REAL averages (Remaining-score Estimate of Average Leg-lengths) applies PDC-average probabilities to a player's remaining score in a lost leg to estimate how many additional darts a player would have needed to finish.
Suppose a player leaves 41 after 12 darts in a leg that they lost. This equates to a 115 average, even though the player likely didn't attempt any doubles. So how many darts would this player have needed to check out in a theoretical scenario?
We know that a PDC Tour Card Holder attempting 41 in 2024 will check out in two darts 37.5% of the time, and in three another 27% of the time.
Yet that leaves another 36% probability that the player will not check out, leaving such scores after that visit as 40, 32, 20 and 16.
Each of those finishes has their own probability distribution of checkouts and scores left, and the process of calculating darts thrown and scores left repeats until 100% of paths result in a finish, even if it requires (in very rare cases) an additional two dozen darts to eventually check out.
After thousands of simulations, we determine that a PDC player will need - on average - 3.61 additional darts to finish from a score of 41.
We can consider this hypothetical leg, in which the player scored 460 points with 12 darts, to be suggestive of a leg won in 15.61 darts, for a REAL average of 96.28.
REAL averages dole out significant penalties to players who do not win their legs. The minimum number of average additional darts needed to check out from the easiest possible finish, 32, is still 2.61 - enough to reduce a player's average by as many as 15 points.
The more legs a player loses, the lower his REAL average will be in comparison with his normal average.
Only 238 Players Championship matches (about 11%) saw the player with the higher REAL average lose the match, a 53% improvement on the ability of normal averages to predict the winner of the match.
Of the 238, the difference between the two players' REAL averages in 151 matches was less than 2 points, and 174 were fought to a deciding leg, indicating that both players lost significant numbers of legs.
A 100 REAL average - a significant achievement, as it suggests that a player would have been on an average pace for a 15-darter, or better, even if they were forced to play every leg of the match to the end - has been achieved by players in only 2% of Players Championship matches, as opposed to nearly 10% of players averaging 100 in the normal calculation.
The advantage of the REAL average is its correspondence with leg lengths. A player with a REAL average of 100.20 is averaging a 15-darter; a player averaging 83.50 is a averaging an 18-darter.
All legs contribute equally to the average and there is no distortion caused by excessive scoring. It does not always predict the winner of the match as played - but it goes further than normal averages in suggesting who was the better player on the day.

